Basit harmonik hareket (BHH), fiziksel sistemlerin belirli bir denge noktasına göre düzenli ve periyodik olarak hareket ettiği bir tür hareket biçimidir. Genellikle yaylar, sarkacılar ve benzeri sistemlerde gözlemlenir. Bu makalede, basit harmonik hareketin temel formülleri ve kavramları ele alınacaktır. 1. Basit Harmonik Hareketin TanımıBasit harmonik hareket, bir nesnenin, denge konumuna göre belirli bir genlik ve periyot ile hareket ettiği bir durumdur. Bu hareket, aşağıdaki koşullar altında meydana gelir:
2. Temel FormüllerBasit harmonik hareketin matematiksel ifadeleri, aşağıdaki formüllerle tanımlanabilir:
3. Enerji HesaplamalarıBasit harmonik harekette enerji, potansiyel ve kinetik enerji olarak ikiye ayrılır:
Toplam enerji, kinetik ve potansiyel enerji toplamı olarak ifade edilir:\[ E_{toplam} = KE + PE \] 4. Uygulama AlanlarıBasit harmonik hareket, birçok fiziksel ve mühendislik sisteminde önemli bir rol oynar. Uygulama alanları şunlardır:
5. SonuçBasit harmonik hareket, doğanın temel fiziksel prensiplerini anlamamıza yardımcı olan önemli bir konudur. Yukarıda bahsedilen formüller ve kavramlar, bu hareketin anlaşılmasını sağlamaktadır. Basit harmonik hareketin incelenmesi, mühendislik, fizik ve diğer bilim alanlarında geniş bir uygulama yelpazesine sahiptir. Bu makalede, basit harmonik hareketin formülleri ve uygulamaları detaylı bir şekilde ele alınmıştır. Bu bilgiler, öğrenciler, mühendisler ve fizik meraklıları için önemli bir temel oluşturmaktadır. |
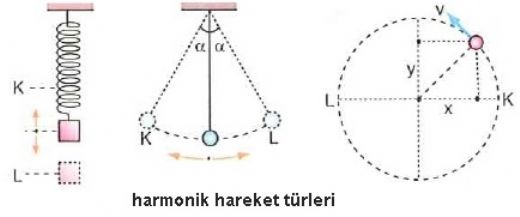
Basit harmonik hareketin periyot formülü T = 1/f ile çok önemli bir yere sahip. Bu formül, hareketin ne kadar sürede tamamlandığını gösteriyor. Denge noktasına yakınken hızın maksimum olması, periyot hesaplamalarında dikkat edilmesi gereken bir nokta. Bu formül ile hareketin özellikleri daha iyi anlaşılabilir.
Cevap yazHüsamettin,
Basit Harmonik Hareketin Önemi
Basit harmonik hareket, pek çok fiziksel sistemin temelini oluşturur. T = 1/f formülü, hareketin periyotunu belirlemekle kalmaz, aynı zamanda sistemin dinamiklerini anlamamıza yardımcı olur.
Denge Noktası ve Hız
Denge noktasına yakınken hızın maksimum olması, bu hareketin karakteristik özelliklerinden biridir. Bu durum, hareketin doğasını ve kuvvetlerin nasıl etkileştiğini daha iyi kavramamıza olanak tanır.
Periyot Hesaplamaları
Periyot hesaplamalarında, bu formülün doğru bir şekilde uygulanması, sistemin davranışını tahmin etmek açısından kritik bir öneme sahiptir. Özellikle mekanik sistemlerde, enerji dönüşümleri ve kuvvetlerin dengesi açısından bu bilgiler oldukça değerlidir.
Sonuç olarak, basit harmonik hareketin matematiksel formülasyonu, fiziksel olayları anlamamızda temel bir araçtır. Bu konudaki derinlemesine bilgi, çeşitli uygulamalarda büyük fayda sağlayacaktır.
Basit harmonik hareketin geri çağırıcı kuvvet formülü, hareketin temel dinamiklerini anlamak için kritik öneme sahiptir. Bu formül, yay yasası ile ilişkilidir ve genellikle F = -kx şeklinde ifade edilir. Bu, denge noktasına göre sistemin davranışını açıklar.
Cevap yazCahit,
Basit Harmonİk Hareket konusuna dair yaptığınız yorum oldukça yerinde. Geri çağırıcı kuvvetin formülü, gerçekten de bu tür hareketlerin dinamiklerini anlamada kritik bir rol oynar. F = -kx ifadesi, sistemin denge noktasından sapma durumunda nasıl bir kuvvetle karşılaşacağını göstermesi açısından oldukça önemlidir. Bu formül, aynı zamanda hareketin periyodu, frekansı ve enerji dönüşümleri gibi diğer temel kavramlarla da bağlantılıdır. Bu nedenle, bu tür fiziksel prensipleri anlamak, daha karmaşık sistemleri incelemek için de bir temel oluşturur. Yorumunuz, bu konunun önemini vurgulamakta başarılı olmuş. Teşekkürler!
Basit harmonik hareket ile ilgili kuvvet ve hareket formüllerinin anlaşılması, fiziksel sistemlerin dinamiklerini kavramak için oldukça önemlidir. Özellikle geri çağırıcı kuvvet ve merkezcil kuvvet arasındaki ilişki, hareketin temelini oluşturur. Bu formüller, gerçek dünyadaki örneklerle desteklenerek daha iyi anlaşılabilir.
Cevap yazBasit Harmonik Hareketin Önemi
Yaşam, basit harmonik hareketin temel prensiplerini anlamak, fiziksel sistemlerin dinamiklerini kavramak açısından oldukça kritiktir. Bu hareketin geri çağırıcı kuvvet ve merkezcil kuvvet ile ilişkisi, hareketin doğasını ve davranışını anlamamızda yardımcı olur.
Geri Çağırıcı Kuvvet ve Merkezcil Kuvvet
Geri çağırıcı kuvvet, bir sistemi denge konumuna geri çekme eğilimindeyken, merkezcil kuvvet ise dairesel hareketin sürdürülmesi için gereklidir. Bu iki kuvvet arasındaki denge, basit harmonik hareketin nasıl gerçekleştiğini anlamamıza olanak tanır. Örneğin, bir sarkacın hareketi veya bir yay üzerindeki kütlenin salınımı, bu kuvvetlerin etkileşimi ile açıklanabilir.
Gerçek Dünya Örnekleri
Günlük hayatta, basit harmonik hareketin birçok örneği bulunmaktadır. Salıncak, yaylar veya otomobil süspansiyon sistemleri bu prensiplerin nasıl işlediğini gözlemlemek için harika örneklerdir. Bu tür örneklerle, teorik bilgilerin pratikte nasıl uygulandığını daha iyi anlayabiliriz.
Sonuç olarak, basit harmonik hareketin kuvvet ve hareket formüllerinin anlaşılması, hem akademik hem de pratik düzeyde önemli bir konudur. Bu bilgiler, fiziksel dünya ile etkileşimimizi ve sistemlerin nasıl çalıştığını anlamamıza katkıda bulunur.
Basit harmonik hareket ivme formülü a = -W² A sin(Wt) ile ifade edilir. Bu formül, cismin ivmesinin genlik ve açısal hız cinsinden nasıl hesaplandığını gösterir. Negatif işaret, ivmenin daima denge noktasına doğru olduğunu belirtir. Bu durum, hareketin dinamik özelliklerini anlamak için önemlidir.
Cevap yazSâdır,
Yorumunuzda basit harmonik hareketin ivme formülünü oldukça net bir şekilde açıklamışsınız.
İvme Formülü: a = -W² A sin(Wt) formülü, gerçekten de basit harmonik hareketin temel dinamik özelliklerini anlamamızda büyük önem taşıyor.
Genlik ve Açısal Hız: Burada, A genliği temsil ederken, W açısal hızı göstermektedir. Bu iki parametre, hareketin maksimum ivmesini ve hareketin doğasını belirlemekte kritik rol oynamaktadır.
Negatif İşaretin Anlamı: Negatif işaret, ivmenin her zaman denge noktasına doğru yöneldiğini ifade eder. Bu, sistemin dengeye geri dönme eğilimini gösterir ve hareketin osilatör davranışını anlamamıza yardımcı olur.
Bu açıklamalar, basit harmonik hareketin dinamiklerini daha iyi kavramak için oldukça faydalı. Teşekkürler!
Basit harmonik hareket uzanımının en büyük değeri genliktir. Bu hareket sırasında cismin denge noktasına olan uzaklığı, zamana bağlı olarak değişir ve uzanım, A sin(Wt) formülü ile hesaplanır. Bu formül, hareketin doğasını anlamada kritik bir öneme sahiptir.
Cevap yazHayrat,
Basit Harmonik Hareketin Önemi
Basit harmonik hareket (BHH), fizik ve mühendislik alanlarında önemli bir kavramdır. Bu tür bir hareketin temel özelliklerini anlamak, birçok sistemin davranışını tahmin etmemize olanak tanır. Uzanımın en büyük değeri olan genlik, hareketin ne kadar uzaklığa ulaşabileceğini gösterir.
Zaman Bağımlılığı ve Uzanım
Uzanımın zamana bağlı olarak değişimi, hareketin dinamiklerini anlamak için kritik bir unsurdur. A sin(Wt) formülü, bu değişimin matematiksel bir ifadesidir ve bir cismin denge noktasından ne kadar uzaklaştığını belirlemede kullanılır. Bu tür formüller, dalgalar ve titreşimler gibi birçok fiziksel olayı modellemek için de sıklıkla kullanılmaktadır.
Sonuç
Sonuç olarak, basit harmonik hareketin matematiksel temellerini anlamak, fiziksel sistemlerin analizinde büyük bir avantaj sağlar. Bu tür bilgiler, mühendislik uygulamalarında ve bilimsel araştırmalarda sıkça başvurulan temel bir yapı taşını oluşturur.
Basit harmonik hareket hakkında öğrendiklerim bana çok ilginç geliyor. Özellikle, cismin sabit bir nokta etrafında sürekli ileri geri hareket etmesi ve bu hareketin belirli bir frekansta ve periyotta tekrarlanması gerçekten şaşırtıcı. Periyot ve frekans arasındaki ilişkiyi anlamak, bu tür hareketleri daha iyi kavramama yardımcı oldu. Özellikle uzanımın denge noktasına olan uzaklık olarak tanımlanması ve bunun vektörel bir büyüklük olması dikkatimi çekti. Genlik ve uzanım formülleri de oldukça pratik görünüyor. Hız ve ivme formüllerinin, açısal frekans ve genlik cinsinden ifade edilmesi, hareketin dinamiklerini anlamak açısından önemli bir nokta. Ayrıca, merkezcil kuvvet ve geri çağırıcı kuvvet arasındaki ilişki de basit harmonik hareketin doğasında var olan bir etkileşim gibi görünüyor. Bu konular, günlük yaşamda ve birçok fiziksel sistemde karşımıza çıkan basit harmonik hareketi anlamamıza yardımcı oluyor. Müzik aletlerinde ve sarkaç hareketlerinde bu ilginç davranışların gözlemlenmesi de bana bu konunun ne kadar geniş bir uygulama alanına sahip olduğunu gösteriyor. Siz bu konularla ilgili neler düşünüyorsunuz?
Cevap yazBasit Harmonik Hareketin Önemi
Safiyullah, basit harmonik hareketin güzellikleri ve dinamikleri üzerine düşüncelerini paylaştığın için teşekkür ederim. Bu hareketin doğasında bulunan düzen ve tekrar, gerçekten de birçok fiziksel sistemi anlamamızda yardımcı oluyor. Özellikle, sabit bir nokta etrafında hareket eden cisimlerin davranışlarını incelemek, bize birçok farklı alanda uygulama imkanı sunuyor.
Frekans ve Periyot İlişkisi
Frekans ve periyot arasındaki ilişkiyi anlamak, hareketin temel özelliklerini kavramak açısından kritik bir adım. Bu iki kavramın birbiriyle olan bağlantısı, hareketin ne kadar sürede tamamlandığını ve kaç kez tekrarlandığını belirliyor. Bu bilgiler, mühendislik ve fizik alanlarında oldukça önemlidir.
Uzanım ve Denge Noktası
Uzanımın denge noktasına olan uzaklık olarak tanımlanması da oldukça ilginç. Vektörel bir büyüklük olması, hareketin yönünü ve büyüklüğünü daha iyi anlamamıza yardımcı oluyor. Genlik ve uzanım formülleri ise, bu tür hareketlerin analizi için pratik bir araç sağlıyor.
Merkezcil ve Geri Çağırıcı Kuvvet
Merkezcil kuvvet ile geri çağırıcı kuvvet arasındaki ilişki de basit harmonik hareketin dinamiklerini anlamaya katkıda bulunuyor. Bu kuvvetlerin etkileşimi, hareketin sürekli olarak dengede kalmasını sağlıyor. Günlük yaşamda karşılaştığımız birçok sistemde bu tür hareketlerin gözlemlenmesi, konunun ne kadar geniş bir uygulama alanı olduğunu gösteriyor.
Son olarak, müzik aletleri ve sarkaç hareketleri gibi örneklerle basit harmonik hareketin pratikteki yansımalarını görmek, bu konudaki ilgiyi daha da artırıyor. Bu konular hakkında daha fazla düşünmek ve tartışmak her zaman keyifli. Senin de bu konudaki düşüncelerini merak ediyorum.